Analysing Remnant and it’s “moon”.

Disclaimer: This analysis includes major spoilers for RWBY up too and including Volume 6. This was also originally written while Volume 6 was airing Between checking the maths and figuring out how I wanted to structure this it has taken this long time. Moreover I’m still figuring out images.

Introduction
Attempting to calculate the density of dust
Quick Summary of Gravity dust breaking Physics
Time on Remnant
Distance between Remnant and the moon
Attempting to weigh Remnant
Revelation
Checking Remnant supports an atmosphere
Measuring Remnant
Rediscovering Dust

1. Introduction

This was originally be the science behind Remnant and it’s moon. Then Volume 6 Episode 3 happened and I realised that even playing hard and fast with the numbers I was going to struggle with explaining how Remnant’s moon has been shattered for thousands of years and somehow held a stable orbit for so long. Sure Gravity dust would be the explaination to some of the finicky numbers and assumptions. That said you have to make assumptions about our very own Earth, Sun, Moon to obtain solvable results and our moon has the advantage of being in one piece. Not wanting to get into pratically impossible maths I dropped it. Then Volume 6 Episode 7 came out and gave use more active use of gravity dust than the rest of RWBY combined and this very almost became something very similar to the ice dust energy capacity already done before on this website. Then Volume 6 ends and I’m hit by a realisation. One I should have made almost 2 years earlier.

The first time gravity dust becomes a real thing is in this scene of volume 4:

This scene is not that special on it’s own. It’s pretty much used as a “oh cool look at all the cool floaty flying rocks and the crystalline structures piercing out under them”. Now every time I’ve seen this scene my mind always goes

“But dust has to be activated by the aura of humans of faunus. Assuming there isn’t people on each of these rocks keeping them up there like that (unofficially confirmed becaused the monsters also living in such rocks would kill any such people) this proves dust also has a passive element to it’s use.” My mind then makes the leap to “Passive gravity dust makes things float and activated gravity dust of what little we saw before Volume 6 Episode 7 makes things heavy.” What I apparently missed in over a year of watchining this scene and dozens of times watching this exact part of RWBY taking me till the end of volume 6 to realise is “THOSE CHUNKS OF ROCK ARE FLOATING.”

2. Attempting to calculate the density of dust

Let me explain why this is a topic in and of itself. For anything to float at a static height like this it has to be neutrally bouyant. This means the density of these islands must be the same as the air they are currently suspended in. Now things like wind, humidity and temperature will also play a role here but the density of air is approximately $1.225 kg/m^3$ . Rock is understandably more dense than air. Logic alone makes this clear but to be completely transparent the density of rock, depending on the type of rock and such, ranges from $1600$ to $3500 kg/m^3$ . Now metal boats float on water despite metal being more dense than water and similarly submarines float in water despite being made of metal. This is because submarines consist of metal and whatever else is inside them whicch is more likely more dense than water with the exception of a large pocket of air (less dense than water). The net density of the submarine therefore is the average of everything inside the volume of the submarine and this is how submarines can go up and down in water, by changing the ammount of water inside the submarine and changing the average density of the submarine. This makes a very intresting poin in what is happening to these islands. To recap:

These islands are floating
This means the islands are neutrally buoyant in air
This means the islands have the density as air.
We know rock is at least 1000 time more dense than air so something finicky is happening due to the gravity dust.

Now taking into consideration how I’ve structured this so far the obvious connection is the metal Submarines float in despie being metal being more dense than water because air is less dense than air so these islands are floating in air becuase of the gravity dust is less dense than air. You would be correct in that I’ve led you think this way. You would also be provably wrong.

All these islands are upright. As they go Gravity dust, Rock, greenery and trees when looking from bottom to top. Also due to the shape of gravity dust if you were to take the cross section from the bottom going up you’d find that they are on average thicker going up. These both go against basic science because of balance. The second is as simple as the fact that balancing a pyramid on it’s point is much harder than on it’s flat edge but because they are floating and not place on top of air this isn’t as damning as the first point. Which most people are probably familiar with in some capacity. If you ever too a plastic bottle into a bath you’ve experienced this. Same with glasses in the sink. But we’ll use a bottle of shampoo as the example here. Plastic (more dense than water) floats in water due to the air (less dense than water) inside it. If you have something in your bottle (shampoo in this case) assuming there isn’t too much of it in there it will still float. But it floats upright. With shampoo in the bottom and the bubble of air above the shampoo (contained within the bottle). Now we can agrue the density of shampoo compared to water but shampoo is definitely less dense than air. Inside the bottle the denser thing goes below the less dense thing. But these floating islands are floating rock on top of gravity dust.

On one hand Gravity dust has to be less dense than air to get the islands to float. On the other balance tells a different story. Sure some islands may have ended up with this orientation due to an equlibrium of balance but such an equlibrium would be unstable. All these islands are in this position, regardless of wind, fluctuation in altitude (which is almost certianly happening), other objects crashing into them. Anything like this would break such a fragile equlibrium in balance. Something more is going on.

Now some people will have thought “Why is he rambling about density this is gravity dust? It’s obviously doing something to gravity.” I even imply that I think it’s something to do with gravity when I talk about this being a confirmation of dust having passive effects on it’s surroundings. So why am I talking about density? To cover all by bases. Because the alternative is basically “And now we break Physics.”

3. Quick Summary of Gravity dust breaking Physics.

So we looped right the way around to the assumption everyone made about this scene. Anti-Gravity. Why didn’t I talk about such a simple solution earlier? As a physicist I only want to go into anti-gravity if there is literally no other choice. Going into dark energy would be preferential and no-one even knows what that is. While I could make up some dark energy arguments as to why the islands are floating this unfortunately doesn’t account fot the other things gravity dust can do. Anti-gravity meanwhile is a doorway to impossible si-fi technologies. Quite literally. While it may not be immediately apparent as to why anti-gravity is a condition for making traversable wormholes… Wait…

Portals are confirmed to be a thing literally two episodes after the floating islands. Or rather this is the first time they are explicitly called portals. The fact I never made this connection sooner is stupid in retrospect.

Gravity dust always has so much potential that I’m genuinely happy that Volume 6 episode 7 exists. Not only in the large gravity dust based combat which occurs but it also demonstrates gravity dust on a more causal level. Being used in construction. Gravity dust always had a level of adaptability where I always found it odd that we never see it used that much. However my opinions of gravity dust have gone from “incredibly versatile” to “literally reality breaking”. To the extent where I would take an adept gravity dust user on my team than literally anyone else that we see in the show. A show with literal gods may I add. To define exactly how effectively gravity dust could be used on Remnant I want to cruch some number on how effective gravity is on Remnant itself. That said let’s start with time.

4.Time on Remnant

To my knowledge analogue clocks appear a grand total of once in RWBY:

This gives us the ability to measure time as we see the “second hand” moving. Unfortunately this doesn’t give us a reference as to “hours” in a “day”, “minutes” in an “hour” and “seconds” in a “minute”. We do know some other things about time. From volume 1 episode 9 we know classes start at 9 and that there was a sprint to classes starting at 8:55. So we can probably assume 60 minutes in an hour. From the same episdoe as the one with analogue clocks (volume 2 episode 3) we also know classes finish at 4. From this I am going to make a leap in logic and suggest the “day”, “hour”, “minute”, “second” relationship on Remnant is the same as it is on earth. Namely 1 “day”, 24 “hours”, 1440 “minutes”, 86400 “seconds”.

Volume 2 episode 3 runs ar a clean 30 frames per second and the “second hand” of the above clocks runs in a smooth motion instead of tick by tick. This scene is on screen for 103 frames or 3.43 seconds in real life. By overlaying the first and last frames of this scene it is possible to find.

Through some simple angle manipulation in 3.43 seconds the “second” hand moves through 17.42 degrees.

A clock has 360 degrees and with the 60 “seconds” to a “minute” relatonship assumed this gives us 6 degrees to a second.

$3.43 seconds = \frac{17.42}{6} = 2.903 "seconds"$

Each Remnant “second” is approximately 0.85 earth seconds. This difference stacks up:

Each Remnant “minute” is only 50.7 earth seconds
Similarly each Remnant “hour” is 50 minutes 44 seconds on earth (3044.3 earth seconds)
Each Remant “day” is 20 hours 17 minutes and 42.5 seconds on earth. (73062.5 earth seconds)

Now why do I want this? With a grand total of 1 exception the moon in RWBY has fixed lunar phase. When I’m talking about lunar phase I’m talking about how much of the moon is illuminated by the sun. So when is this exception. The yellow trailer. Honestly I’m half tempted to call this scene retconned. Partially because it’s been so long. Partially because I can argue that the sun in the yellow trailer isn’t actually the sun. I get the imagery and all but the sun isn’t nearly bright enough in this scene in my opinion. So Remnant’s moon phase equlivalent comes from it’s rotation. Which I’m 90% sure I can explain and while an intresting point I don’t really want or need to go into the semantics of the intermediate axis theorem for what I want the moon for.

N.B. From this point I am going to be measuring and doing maths in earth time seconds because that’s how the equations are desgined to work.

Kepler’s third law is that

$R^3 \times 4 \times \pi^2 = T^2 \times G \times M$

Where $R$ is the average orbit radius, $T$ is the orbit time $G$ is the universal gravitational constant and $M$ the mass of the larger object. This can be re-ordered too:

$M = \frac{4\pi^2R^3}{T^2G}$

Only we can’t weight Remnant because we don’t know Remnant’s moon’s orbital distance. Or so you would think.

5. Distance between Remnant and the moon

Volume 6 episode 3 the god of darkness travels to the moon. The episode runs at 25.03 frames per second and it takes 20 frames to get to the moon. Now owing to the fact the god of darkness is… well… a god. The speed of darkness is presumably the speed of light. This gives us

$239,546,511 m$

This is only the distance between Remnant’s surface and the moon. $R$ in Keplers law requires the distance between the centres of both objects so this is only a part of the distance. If

$R=r_1+r_2$

and $r_2$ is $239,546,511 m$ we still need $r_1$ or the radius of Remnant itself.

6.Attempting to weigh Remnant.

Now I have linked to this in passing before. https://www.reddit.com/r/RWBY/comments/65gkbt/how_much_gravity_does_remnant_have/ I’m quite happy with the numbers here and see no reason to redo it. I am however going to take it a few steps further.

$g = 6.42803 m/s^2$

Another equation I’m going to use is the acceleration due to gravity near a planets surface:

$g = \frac{G \times M}{r_1^2}$

$M = \frac{g \times r_1^2}{G}$

Some manipulation later:

$\frac{4 \pi^2 (r_1+r_2)^3}{T^2} = g \times r_1^2 = M \times G$

Now I could work through how to solve this for $r_1$ given we now know $r_2$ , $g$ and $T$ is the same time as a Remnant “day” or I can plug said numbers into a computer and it can do the work for me. Fun fact though. We don’t get real answers.

We either get:

$r_1 = - 72941900m$
$r_1 = (111739000 + 419479000i) m$
$r_1 = ( 111739000 - 419479000i ) m$

Negative distance doesnt make sense and well complex numbers imples something much more is at work here (for those that don’t know $i^2 = -1$ ). To interpret this better I am going to attempt to work out the mass of the planet from the $G \times M$ term.

$M = 5.12438 \times 10^{26} kg$
$M = (-1.57451 \times 10^{28} + 9.02884 \times 10^{27} i) kg$
$M = (-1.57451 \times 10^{28} - 9.02884 \times 10^{27} i) kg$

Now we can eliminate the latter two. Why? Well imaginary mass is a mathematical construct. If it existed it an object with an imaginary mass would only ever travel faster than the speed of light and by extension backwards in time. Those that like their si-fi jargon tachyons are particles with complex mass. Now you can argue about special relativity, refrence frames and such but this would require everything on Remnant, Remnant’s moon, Remant’s sun, the stars seen on Remnant all to possess complex mass. Dust only operates inside Remnant’s atmoshpere and by extension this complex mass is more of a universal quirk than a product of gravity dust can can be systematically eliminated.

So we are left with $M = 5.12438 \times 10^{26} kg$ and $r1= -72941900 m$ . Only not really. This equasion that the moon is too far away to be orbiting Remnant. So something’s gone wrong. Specifically one of the variables used in the equation has been defined wrong. This is where we run into something I wasn’t aware I could even do until this point.

7. Revelation

Using $\frac{4 \pi^2 (r_1+r_2)^3}{T^2} = g \times r_1^2 = M \times G$ has a few in built assumptions. Most of these were already covered when introducing keplers law and acceleration at the surface of a planet equations. Equating the two together however requires one further assumption. $g$ and $M$ must corispond to the same object and this object must be the heavier object. If you were to use this equation for the values for the sun and the earth but use $g$ as the acceleration at the surface of the earth $T$ as the orbital period of the earth and $r_2$ as the seperation between the earth’s surface and the sun you get the following solutions.

$M = 1.8522272062663572 \times 10^{30}kg$ , $r1 = -3.549836330636958 \times 10^9m$
$M = 2.1471063869205464 \times 10^{30}kg$ , $r1 = 3.821976234785443 \times 10^9m$
$M = 8.94877445609537 \times 10^{39}kg$ , $r1 = 2.4674194367917662 \times 10^{14}m$

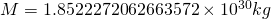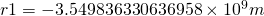
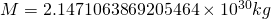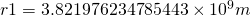
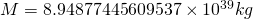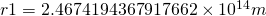
Why am I telling you this? Especially if I’m putting the wrong numbers into the equation. $g$ would need to be the acceleration at the surface of the sun because the sun is heavier than earth for the equation to work. Well the first result gives us a negative $r_1$ value. It also happens to give us a value for $M$ which is within error of the mass of the sun. Now I’ll admit I don’t 100% understand why this happens but you can do similar things with the Earth/Moon relationship (using $g$ of the moon to find $M$ of earth) and even the Pluto/Charon relationship. I assume it has something to do with the fact that gravity is a central force or Newtons laws. But I’ve checked it multiple times and it is self consistent.

So we have accidentally stumbled across something. Remnant doesn’t weigh $5.12438 \times 10^{26} kg$ at all. We accidentally and unintentially measured the weight of “Remnant’s moon” and along the way discovered that “Remnant’s moon” isn’t orbiting Remnant but rather it’s the other way around. Remnant is a moon orbiting around the planet named “Remnant’s moon”. This inversion between habitable moon, uninhabitable planet is the opposite of our own Earth/Moon relationship and I find it quite intresting. This could also be used to explain why Remnant’s moon is shattered but didn’t break down into a ring. Now if we want do discuss why Remnant’s is habitable and why it’s moon isn’t we reaching the edges of my physics knowladge and a part of physics where equations only gives you estimates which are known to be quite bad.

8. Checking Remnant supports an atmosphere.

For the purposes of checking weather Remnant would have an atmosphere despite Remant’s moon being the heavier object we need two equations.

$V_{escape} = \sqrt{\frac{2GM}{r_1}}$

This equation is used to calculate the escape velocity of an object in space. If you travel faster than this speed you leave the plannet.

$v_{rms} = \sqrt{\frac{3k_bt}{m}$

This equation is used to measure the average speed of gas. $k_b$ is a constant. $t$ is the temprature and $m$ is the mass of the gas particle. So for a planet to hold an atmosphere

$V_{escape}<v_{rms}$

Which after some manipulation, and making the assumption that the mass of Remnant and Remnant’s radius is positive (which must be true), becomes:

$0<t<\frac{2mG}{3k_b} \times \frac{M}{r_1}$

Therefore:

$\frac{t\times r_1}{M} < some\_constant$

We now know that Remnat’s moon has a larger mass so either the average temprature or the radius of Remnant is smaller than Remnant’s moon. Now Now it is possible to talk about the average temprature. It’s just that the results of the equations are generally incorrect. Planets with an atmosphere will tend to have a higher average temprature than predicted and Planets without an antomsphere will tend to have a lower average temprature than predicted. As an example of this the equation predicts earth’s average temprature as -18C when in reality is is closer to 14C and it predicts that our moon has a temprature of -37C when it is actually closer to -76C. So the only real conclusion we can make is that Remnant has to be smaller than Remnant’s moon. Exactly how much smaller depends on the temprature and Mass of Remnant as well so it’s not particularly the easiest thing to calculate but it is reasonable to assume that in order to counteract the fact Remnant’s moon will be cooler (due to a lack of atmosphere) and Remnant’s moon is heavier (as proven) Remnant is going to have to be noticably smaller than it’s moon in order to be able to hold it’s atmosphere. So we’ve looped around to an issue we had earlier. We still don’t know what $r_1$ is.

9. Measuring Remnant

The map of Remnant is a fairly re-occuring theme throughout the show. So it’s not all that difficult to find one. There is of course an issue with measuring planets with map’s like these:

It comes from the simple fact that they are a pain to use. Primarally due to the fact there is no easy way to convert the surface of a sphere to a rectangle. This is why you end up with weird things like Greenland and South Africa looking similar sizes when South Aftics is 8 times the size. A more accurate representation would be something like this.

Which is something I quickly made up in order to prove a point. Granted the distortion of the distance I’m going to be measuring isn’t all that big but I want to be as accurate as possible. Regardless first we arent starting with this map but rather:

Why do I want this? Well in Volume 2 they go on a train. While we don’t know the exact route of this train from what we see of the underground tunnels it is a rather straight line, so we don’t have to worry about the path much but rather where the start and end are located. We know the train starts

“In the southeast. Just outside the kingdom.”

This is assumedly the red circle in the lower left of this map. We also need to try and figure out where the train ended up. Judging from the presence of shops in their final destination this implies the commercial district. Between that the large open “town square” like space and what little we can see of the road layout in this map I’m tempted to say the small left circle located in the commercial district section (near the upper class section). This image is 940 by 580 pixels. A line drawn between the centermost points of these two picels is 419 pixels across and 278 pixels up. With some basic trigometry later 502.8 pixels in length.

That’s great now what? Well we go through Volume 2 episode 11 and try to determine how much time was spent on the train. You can argue that between cuts and events happening simultaneously this is impossible but the best estimate I’m taking is scenes where Yang is seen on the train.

3:06-7:00 = 296s
7:53-9:08 = 75s
11:23-11:56 = 22s
12:27-13:34 = 70s
14:14-14:27 = 13s
476s = 7 minutes 56 seconds.

All we need now is the speed of this fictional train. There is unfortunately no easy way to do this.

This tunnel has many repeating segments and it is possible to measure any and all of the vertical dimensionality of this tunnel but between perceptive, camera angles, camera focus and the fact everything is in motion there is no way to take any horozontal measurements. I can work out the ratios between two distances all day but lacking a single horozontal measurement these ratios are useless. So we skip forward. 4 years and a different continent later we finally get the perfect view of a train. If you neglect the fact this is the wrong train and a completely different scene.

From the front of the train we see that the train has at least a very similar make. So between knowing Ruby’s height is 1.57 meters and measuring pixels these armored segments are 10.46 meters long. Another scene of this train reveals 4 armored segments to a carriage (unfortunately there isn’t a single easily obtainable frame that shows this) so 41.84 meter long carrages. This scene:

While not immediately apparent suggests that 5 carriages can fit in a segment. Assuming that carriages of both trains are of similar size. This leads to each segment being 209.2 meters long. The episode runs at 29.97 frames per second it takes 36 frames for the train to travel a segment so 1.2 seconds to travel a segment, so the train is traveling at 174.16 meters per second or just shy of 400 miles per hour. For reference terminal velocity for a human is around 122 miles per hour and the world record for a maglev bullet train is 375mph and this train has wheels. We are going to keep this value though. While I don’t have the characters to explain exactly why so I’m going to wave my hands and say the train has some kind of dust powered aerodynamic shielding that both let’s it reach these speeds and doesn’t rip the characters off the top of the train.

Trip length: $174.16 \frac{m}{s} \times 476s = 82.9 km$

Horizontal distance of trip: $\frac{82.9}{502.8} \times 419 = 69km$

Horizontal pixel size: $164.86 m$

Island of patch width: $164.86 \times 99 = 16.32km$

Map of remnant circumference at island of patch: $1530.94km$

Now I’m going to introduce the measurement distortion from rectangle to sphere surface.

First the map of Remnant is 938 pixels wide. A measurement of 10 pixels corresponds to 2.5 kilometres so the map is 235.8 kilometres wide at this latitude. Through coordinate conversion we know that

$r = \sqrt{x^2+y^2+z^2}$

Where r is the radius of sphere. z is the height the measurement is made at and given the measurement for circumference at that height we can work out the value for x given any y so letting y=0

$x = \frac{c}{2 \times \pi}$

The measurement of height also has to be given as a fraction of radius.

$z = k \times r$

So:

$r = \sqrt{ \frac{c}{2\times \pi}^2 + (k \times r)^2}$

$r = \frac{c}{2\times \pi \times \sqrt{1-k^2}}$

Well we’ve already measured c in this equation. c=1530.94 kilometres and have all the information we need to find k

The measurement is made at 262 pixels down a 528 pixel tall image. We want the displacement of the measurement from the centre of the image as a fraction of half the image’s size so

$\frac{528}{2} =264$

$264-262 = 2$

$\frac{2}{262} = k = \frac{1}{131}$

We now have everything we need so:

Remnant radius: $\frac{1530.94 km }{2\times \pi \times \sqrt{1-\frac{1}{131}^2}} = 243.66 kilometres$

Good news. Remnant is small. Bad news. Remnant is tiny. The radius of the earth is 6371 kilometres. Indeed an astral body formed mainly of rock needs to have a radius of 600 kilometres otherwise it won’t collapse into a spherical shape. While you can argue that gravity dust could rectify this tiny sphere problem Remnant is just far too small.

But it doesn’t stop there. Now we have the radius we can go back to this equation:

$g =\frac{ G \times m}{r^2}$

We know g, G and now r so we can find:

m= $5.718142401989006 \times 10^{21} kg$

This reinforces what we proved earlier in that the mass of Remnant’s moon is larger than the mass of Remnant itself.

M_Remnant = $5.71814 \times 10^{21} kg$
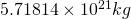
M_R’moon = $5.12438 \times 10^{26} kg$

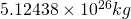
However we do run into a slight issue now. Density is calculated through the mass of an object divided by it’s volume. We have everything we need to determine the density of Remnant. But before I do some other values to compare:

The density of water: 1,000 kg/m^3
The average density of the sun: 1,410 kg/m^3
The density of our moon: 3,340 kg/m^3
The density of earth: 5,515 kg/m^3
The density of iron: 7,874 kg/m^3
The density of Osmium (the densest known material under normal conditions): 22,590 kg/m^3
The density of Hassium (the densest theorised metal): 45,000 kg/m^3
The density of the middle of the sun: 150,000 kg/m^3
The density of the core of a thermonuclear weapon as it explodes: 1,560,000 kg/m^3
The density of Remnant: 5,603,000,000 kg/m^3
The density of a white dwarf star: 10,000,000 kg/m^3 to 10,000,000,000 kg/m^3

Yea so there’s something afoot here. Good news is that the density is still in the realm of possible with gravity. Better news is that if you let the core of remnant be denser than the quoted value it should still be able to support having normal materials with normal densities on the surface. Bad news is either A) Remnant should be far hotter than it is or B) Remnant is several billions of years old. We aren’t talking the earth is 4 billion years old age. We are talking comparable to the current age of the universe old. So RWBY could be set in the far off future. However if Remnant is so old either Remnant’s sun is of comparable age (in which case it would have similarly burnt itself out) or Remnant was captured in a different star’s orbit. Now it’s certainly possible for stars to steal planets from other stars but for this to happen and the stolen planet end up in the new star’s goldilocks zone is unlikely. So rather than entertain this idea we loop back around to A and ask the question where is all the energy? Remnant should be so hot that it can’t support liquid water let alone be mainly ocean. If the energy isn’t heating up Remnant then what is it doing. It’s not like Remnant has an dense form of energy storage that’s in exceptionally high abundance.

Wait…

10. Rediscovering dust

No seriously. It took me a couple of weeks to figure out how I wanted to continue from here. Because as much as I can continue we are rapidly hitting the limits of how far I can go. Let’s say that the Remnant’s core is comparable with the upper limit of a white dwarf. On earth the density of the surface is only $2670kg/m^3$ . It has a higher density towards it’s core which is how it ends up with an average density of $5,515 kg/m^3$ . So assuming that the surface of remnant has a similar density to the surface of earth and Remnant’s core is towards the upper limit of a white dwarf star.

$10000000000 \times a+2670 \times b = 5603000000 \times (a+b)$

Remnant’s core accounts for little over 56% of remnant’s Volume (from finding a/a+b). By extension Remnant’s crust accounts for little under 44% of Remnant’s Volume

So how thick is Remnant’s crust.

$dV = \frac{4}{3} \times \pi \times dr^3$

$dr = (dV \times \frac{3}{4} \times \pi)^{1/3}$

where dV = 43.97%

dr = 0.47

Average crust thickness: $dr \times 243.66 = 114.94 km$

By comparison Earth’s crust varies between 5 and 70km (depending where you are). Now with this we’ve reached the limits of what I can mathematically describe so I move on to summarising what we’ve assumed and how that creates dust.

Long long ago Remnant was a dying star. One god sealed the power of this dying star. Another took the dying star and made a planet around it. The first god made a “planet” near the dead star to relegate the dead star “planet” into a moon and together they took their planet moon system to orbit a different star. Couple of legends about the creation of man and Grimm later a single individual manages to annoy the gods. Not only do the god’s leave but before they do they 1. Commit genocide. 2. Destroy the planet the dead star “planet” was orbiting around. This wrecks havoc on the dead star “planet”. Between the flaming debris raining down on the “planet”, the gravitational turmoil, the loss of tidal locking (Aside while when I say tidal locking you probably think about the ocean tides, planets without oceans tidal lock due to their molten cores) probably a few dozen other things destroying Remnant’s moon did. The Crust of Remnant was cracked and the sealed away dead star was exposed or at the very least started breaking it’s way through the crust in various points (insert something about volcanos, and continental drift and such here but geography isn’t my field so just pretend there’s some enlightening thing about this here). Many millions of years later a species not dissimilar to the initial killed species somehow manages to evolve and discover this sealed power. Badda bing, badda boom, Dust. “Why does Dust have different forms if it all comes from the core?” Something about reacting with materials on the way through the crust, or inconsistencies with how the gods sealed the star away, or the star had multiple seals. It’s Dust, I don’t know.

Idle Poderings and Creative Brainstorming

Science in fiction » Analysing Remnant and it’s “moon”.