Science in fiction » A mathematical analysis of Dust (RWBY). (Out of date)

NOTE: This page is now considered out of date. It is kept up for transparancy’s sake but the most recent work on this piece can be read here.

Disclaimer: This was originally written up early 2018. Between checking the maths and figuring out how I wanted to structure this it has taken this long time. Also I’m still figuring out images so they may or may not work. With that said this particular text assumes no prior knowledge of RWBY and only contains Volume 2 spoilers. For a show with 6 seasons/volumes at time of wtiting and taking the overarching plot into consideration this isn’t too bad.

1. An Introduction to RWBY and Dust.
2. Getting started.
3. Ice dust.
   1. Determining the volume of Ice dust used
   2. Determining the power of the dust sample
      1. The Volume of Gambol Shroud
      2. Blake’s Volume
      3. Volume of everything else
      4. Total volume generated
   3. How to create ice?
4. Best case scenario
5. Worst case scenario
6. A realistic attempt

1. An Introduction to RWBY and Dust.

For the uninitiated RWBY is an online show made by the American company (Rooster teeth who I am not affiliated with) and takes place on a planet known as Remnant. Excluding a small number of cities most of Remnant is dominated by monsters referred to as Grimm. Due to the hostile nature of these Grimm technology on Remnant is different than it is on earth. Despite possessing enough technology to not only make guns but incorporated guns into almost any type of melee weapon, melee weapons are the primary effective tool against Grimm. Specifically, in the hands of trained fighters called Huntsmen (and huntresses). The four main settlements have an army and a police force but for the most part Huntsmen represent the main defensive force against the creatures of Grimm. In my personal opinion the main difference between Remnant and earth is not the ni on constant threat, but instead a resource called Dust.

Dust is important in RWBY. To the extent that we are given an info dump about dust before we even meet the main character. Dust is referred to as a “a naturally occurring energy propellent” and holds a very similar role to oil in our world. With some differences. The first is that Dust is crystalline in nature so where oil is pumped Dust is mined (making it closer to coal during the industrial revolution in this respect). On Earth 50% of the oil we use goes into fuels, but it also finds uses in plastics, medicine and clothing. On Remnant Dust comes in many different forms, each distinctly different.

The best way to describe the types of dust would be to think of an element system. Fire dust when used makes fire. Earth dust when used makes earth. Air dust when used makes wind. Water dust while confirmed to exist hasn’t actually been shown in the show but would assumedly make water. From here Dust can be combined “both artificially and naturally” into other types of dust. While some of these are expected, such as ice and steam, others are much more abstract such as gravity and hard light. On one hand I’m frustrated that there is no official list of all the dust types yet. On the other there is one thing I found particularly interesting about how Remnant treats dust.

“It was crazy. We have dust … but I mean there’s no such thing as magic.”

Remnant does not perceive the ability to manipulate gravity itself using the right coloured crystal to be magic. Maybe they did at one point in time but modern Remnant as we watch it in the show is technologically advanced enough that to them it isn’t magic. It’s a science.

Now there’s tonnes of interesting things when it comes to dust’s existence. From a sociological standpoint certainly but that isn’t my strong point. From a scientific standpoint Dust is ridiculous. For a quick reference gravity dust can break the speed of light if used correctly. That’s the level of reality breaking we are talking about here. The other thing is Remnant seems to be de-sensitised to this. They use the stuff everywhere. They have shops casually selling the stuff in bulk. But there is some reasoning. For starters it’s exceptionally convenient. No need to worry about large power plants to convert fuels into electricity, just use electricity dust. A part of me wonders if they discovered fire by rubbing together sticks or by using the red crystal first. No need to take drinking canteens on a trip, take water dust. The stuff you’ve packed for your trip still heavy? Gravity dust. So on and so forth. The second and main reason for this passage existing is that the sheer power held in Dust puts Earth fuels to shame.

2. Getting started

Exactly how powerful is Dust. Well the short answer is, more powerful than anything you’ll likely get your hands on but ultimately it varies. While I could just say here’s, a number let’s compare it to real life examples you’d be taking my word on the number. So instead I am going to go through all the workings starting with the logic.

We are going to be calculating the energy density of ice dust? Why. Well the first reason is that it is the most commonly used dust in RWBY by far. The second is that it is possible to get a lot of the numbers from the same episode and the third is that this is not the first time I’ve calculated the energy density of ice dust. This will be the third and while this will be the most in depth analysis on ice dust and therefore more accurate than the previous two times I can sanity check the numbers against the two more casual studies. With that said let us begin.

3. Ice dust

In season 2 episode 11  https://youtu.be/CUYhvPoxuas?t=478 (Episode link timestamped) we see Weiss (character in white) giving Blake (character in Black) a selection of dust Vials. This is arguably the best situation for determining the energy capacity of any dust type as from the previous link we can determine the dust’s volume and from later on in the same episode (Here: https://youtu.be/CUYhvPoxuas?t=611 ) we see the only fight where Blake uses any significant amount of Dust as of time of writing. It doesn’t matter which of the colour of dust ice dust actually is as all the vials are the same size. Which leads quite nicely into part a.

3a) Determining the volume of Ice dust used.

Luckily for the purposes of this particular part of the maths most of the hard work is already done. A 1:1 3D model of Gambol Shroud (Blake’s weapon) already exists https://www.myminifactory.com/object/3d-print-gambol-shroud-rwby-20990 so it is simply a measure of opening up the model in some 3D software and making an educated guess as to how far in the pistol mechanism an ammo clip goes.

Estimated Ammo clip dimensions: (mm)

Aside: The aforementioned 3d model is made for the purposes of 3d printing and most 3d printers only have an accuracy of 0.2 when printed. 

Next task is to determine how many dust vials would fit in Blakes’s ammo clip. While @8:01 would imply that there are 6 dust vials in the clip a few instants earlier shows that each dust vial is 29.5 pixels wide and 85 pixels worth of un-used space. Meaning that Blake’s ammo clip could have held 8 dust vials. Some simple maths later we obtain

Dust Vial dimensions approximate: (mm)

This however has two issues. The first is “what shape are the dust vials?” This is simple enough to answer. Cylinders. Bullet’s are cylindrical, the dust is going into a gun this simply makes sense. Which poses a problem as according to this same math the 15.37 and the 13.063 are both diameters. However as the measurement of 15.37 was simply an estimated depth of how far into a gun a magazine goes ammo clip rather than a direct measurement and a 2mm deviation between that and the actual measurement isn’t too big in the greater scheme of things. As for the second the second dimension in the above measurement needs to be lessened slightly as so to make space for the walls of the clip itself. Unfortunately there is no good angle to get this so any reductions are estimates at best. Even worse looking at the lengths of 13mm calibre bullets doesn’t help in this matter as the smallest length bullet of this size, the 56 Spencer has a case of 39.24. (This doesn’t invalidate the firearm’s of remnant entirely as it will be later proved that dust is far more powerful than modern propellants.) The best that we can estimate about this is to take the measurement’s from a real magazine https://www.bevfitchett.us/ar15-m16-2/images/3125_12_161-lower-receiver-dimensions.jpg and assume that this magazine has to have walls of similar thickness.

Dust Vial Dimensions Final: (mm)

From here it is only a question of simple math to obtain the total volume of the dust canister:

For reference a medical teaspoon is 5ml.

Aside: What about the dust container itself?

This is an interesting conundrum in and of itself. Dust normally coming in three forms, cut crystals, uncut crystals and powdered crystals. There are also ways of interpreting what the container itself is. Either the canister is glass in which case the dust must be powdered (as dust crystals are repeatedly shown to be hexagonal) or the canister follows a standardised colour coding, in which case it is impossible to tell how much dust is inside as the canister itself could be housing empty space inside it. Fortunately due to the amount of times we see these canisters throughout the show, of various sizes and how the colours match the cut/uncut crystals exactly in other scenes we could assume glass of negligible thickness or we could consider that powdered dust could be compressed into pellets before use and therefore would retain it’s shape without a canister to hold it.

3b) Determining the volume of ice generated

What happens to the dust is incredibly simple to explain with words. But rather difficult to describe with numbers. Blake, using dust, effectively creates an ice statue replica of herself. Here is where thing’s get a bit more complex. Fortunately, we have a value for Blake’s height, alongside all other characters found in this season of RWBY from a height chart. https://vignette.wikia.nocookie.net/rwby/images/f/f1/Sizechart.jpg/revision/latest?cb=20140913091405 A minor issue with this is that in this image Blake is wearing heels and a bow, something quite easily rectified. The real problem is that for the calculation we don’t need Blake’s height. We need Blake’s volume or more specifically we need the volume of the ice statue Blake makes of herself. This means Blake, her hair, her weapon and her clothes and so on.

i] The Volume of Gambol Shroud (Blake’s weapon).

This is thankfully a rather simple process of opening up the 1:1 model of Gambol Shroud, piece by piece and simply reading off the volume before adding them together being careful not to count duplicates (as so to only make one Gambol Shroud)

ii] Blake’s Volume

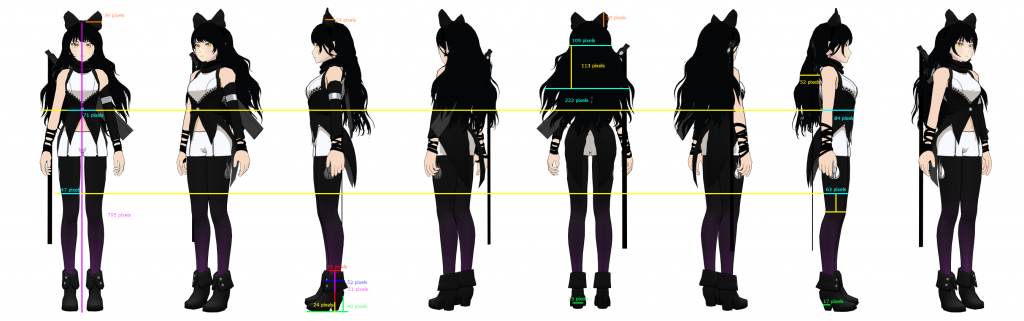
While not immediately apparent as to why we are now going to make various measurements of Blake’s body. Doing this all at once so that all the measurements are in the same place. Blake’s height from toe to head (in heels) is 1.68 meters. In a character reference this same length is also 795 pixels. After some working out where Blake’s leg enters the heels we find that they add an additional 24 pixels to her height which corresponds to:

Added height:

Blake’s height:

Two more required measurements require simple single measurements that only require a little maths to determine and Blake’s abdominal circumference and Thigh circumference:

Taken at the measurement of the belly button (which is approximately the height of the elbow)

Minor axis (across front of chest):

Assuming arms are relaxed and the back straight the backs of the arms align with the back of the back:

Major axis: (side view of stomach):

Circumference of an ellipse:

Abdominal circumference:

Thigh measurements taken at 10cm above the knee

10cm = 47 pixels

Minor axis (front view):

Major axis: (side view):

Thigh circumference:

Which leads us to why have we taken these measurements at the beginning of this section? We need Blake’s Volume and while it would be possible to transform Blake into a number of Cylinders and spheres not only would this require a lot more measurements than those above but has a rather wide margin for error. Instead we run off the assumption that humanoids on Remnant have approximately the same proportionality as humanoids on Earth. Which then Leads us to how do we measure the Volume of a human without putting them under water and measuring the displaced liquid. From: http://www.dtic.mil/dtic/tr/fulltext/u2/628948.pdf

Simplifies this dramatically. Now we only need the Surface Area, Weight and Height of Blake. We already have Blake’s Height so the next question easiest of the three to measure is Weight. Only we can’t put a fictional character on a set of scales. Instead we have to rely on more research. This time from: https://digitalcommons.unl.edu/cgi/viewcontent.cgi?article=1006&context=usnavyresearch

Blake’s Weight =

Aside: This is not the first attempt of measuring weight. The first method used was this one (http://www.eurecom.fr/en/publication/3189/download/mm-publi-3189.pdf) which while more accurate is not suitable for measurements under 35kg. This also reveals that Blake is severely underweight, practically anorexic. (BMI around 11) Moreover Blake is hardly the odd one out in this situation. There are of course two ways of looking at this. First is that the assumption that humanoids on Remnant and Earth are proportional is completely wrong. Most likely due to the animation style of RWBY and the fact that animation in general has a way of giving females unnatural proportions in the first place. The second way of looking at it is that this is in fact true. For starters Remnant isn’t earth. An example of this is that gravity on Remnant is roughly Two thirds of that on earth: https://www.reddit.com/r/RWBY/comments/65gkbt/how_much_gravity_does_remnant_have/

Even then the characters in RWBY repeatedly propel themselves with gun recoil, jump incredible distances, perform impossible feats of climbing up falling debris. Blake repeatedly has the ability to pull herself around with a piece of ribbon. Sure pulling herself around at the speeds she does could be considered a feat of strength more but the fact the ribbon is more than capable of carrying her weight is more impressive than it should be. The ribbon being made of an interesting material in and of it’s own rite, channelling aura through weapons having an impressive effect on it’s durability or Blake (and for that matter everyone) is really light weight. Sure this is circumstantial at best but the alternative is to assume Blake has the same build as others her age and making the assumption that she is the same as the average weight for her age and gender here on earth (which as a trained fighter is unlikely).

The last requirement for volume is Body surface area which thankfully is simply substituting numbers into equations if height and weight are known. From https://www.calculator.net/body-surface-area-calculator.html?csex=f&bodyweight=29.3&bodyweightunit=kilogram&bodyheightfeet=&bodyheightinch=&bodyheight=163&x=123&y=15 and averaging.

Surface Area:

This finally giving way to:

Volume =

Blake Volume =

iii] Volume of everything else

All we have left is to determine the volume of the rest of Blake’s constituent outfit and other yet unmeasured volume. All we can really do for this is take measurements, assume shapes for each part.

The main addition of volume from the shoes come from both the heels and the effective “collar” around the ankle. The heel is the easier of these two so starting with that one:

Assuming the heel is a cuboid: (It’s not. See the aside)

pixels

As for the shoes collar assuming that it’s a tube (cylinder with a cylinder taken out of it):

Pixels: 52 diameter – 29 diameter and 51 height

Cm: 10.99 diameter – 6.13 diameter and 10.78 height

Cylinder:

So for a single shoe:

For both shoes:

Next for the bow.

Assuming one side to be a triangle based pyramid.

pixels

For entire bow:

Finally for the hair:

Assuming a trapezium based prism

Pixels: (109 vs 222) * 113 * 52

Aside: Why not clothes?

The first and main reason for not including clothes in this calculation is the fact that Blake’s clothes are for the most part rather form fitting and do little to add volume to Blake’s ice statue. The only exception to this would be the two pieces of fabric that look like they come from a penguin tail tuxedo. As to why these aren’t included the answer is that from the above calculations above are almost certainly an overestimation of volume and the heels of the shoes due to treating the typically semi-elliptical prism as a cuboid leads to an overestimation of volume. Similar arguments can be made by each part calculated through assumed shapes above. By neglecting the volume added to the statue from this fabric it is hoped that the overestimation of these can be offset somewhat.

iv] Total volume generated

Now it’s just a matter of adding everything up to get the final total volume of the ice statue:

Quick note:

After this point maths calms down a lot and there is practically no assumptions that introduce error into the maths itself. We do have two more assumptions to make. The first is a rather nice assumption. We are going to assume the ice statue Blake make’s is solid. This assumption is justified for two reasons. For starters Roman (the person Blake fights in this scene) struggles to retrieve his weapon from the statue so any thickness the statue does have, is sufficiently thick to not break under a little force. The second reason we can make this assumption is because we actually see the statue being broken a few moments later and as far as I can tell from going through screenshots of the debris the only hollow pieces are the frozen pieces of clothing which would have had frozen Blake’s body pieces in them. This does add an interesting fact in that we would have of overestimated the volume of ice given the statue was accurate enough to leave air gaps between clothes and the main body had we calculated the volume of the clothes as an additional layer over Blakes’s body (which was the initial plan). The second assumption we have to make is going to have a drastic effect on the final result and we have no way of sanity checking it.

Right so turns out spending months editing this up means that when I upload it I come across new information in under a week. I somehow managed to find a model of Blake. Which shows that body, hair, clothes (basically everything excluding weapon) has a volume of 99.9603 litres. Which totals up to 100.756607 liters. Making all the calculations off by a factor of 2.6. I don’t want to write everything all at once so I will slowly correct. In blue for transparency’s sake.

3c) How to create ice?

Strangely despite the number of equations involved in calculating Volume and all the assumptions made which could very easily introduce a large amount of error this isn’t the biggest source of error in working out the energy density of dust. The biggest degree of error actually comes from figuring out where the ice comes from. If I said where does ice come from normally the answer is easy. Frozen water. Pointing at an activated ice crystal and saying where does that ice come from is significantly more difficult. I can theorise but unfortunately we don’t know enough to say that any method is definitely certain. Ordered by most reasonable energy wise (with further notes below each):

• Water is stored, super compressed in an ice crystal at 0 degrees Celsius
  • While dust has to be activated in order to do things such as make statues of ice we see gravity dust, with no reasonable way of having been activated, floating. Gravity dust when activated makes things heavier seems to have a passive element where it can float efficiently enough it can also carry stuff with it. Ice dust having a passive element where it is cool isn’t entirely unthinkable.
  • To do this water would have to be compressed greater than 10,000 times when stored in a dust crystal
    • At this density hydrogen would begin to fuse into other elements which would not only ruin the chemical composition of the resulting “ice” but also mean that the dust crystal is continually heating up (like the sun) not cooling down (as this point assumes).
• Water is stored, super compressed in an ice crystal at room temperature.
  • This doesn’t solve the compression issue.
• Water vapor is drawn in from the surroundings and frozen.
  • At room temperature and 100% humidity there is 17.3ml of water in every 1000l of air (https://www.engineeringtoolbox.com/maximum-moisture-content-air-d_1403.html) Granted in this scene they are underground and to go from outside southeast Vale to the commercial district (which is presumably where the train is headed given the number of shops that are at the trains destination) they would have to go under at least one river (http://vignette1.wikia.nocookie.net/rwby/images/4/4c/ValeMap.png) so I can only assume humidity is quite high but even assuming humidity is 100% to make that much ice the ice crystal would have to attract the water vapor from a Olympic swimming pools worth of gas, in practically an instant, and do so while contained a train carriage (which is 100 times too small).
    • 38696.72/17.3
    • 2236.8 m^3 minimum air required
    • Olympic Swimming pool volume = 2500 m^3 (https://en.wikipedia.org/wiki/Olympic-size_swimming_pool)
    • Train Volume: 212.5 m^3 (https://en.wikipedia.org/wiki/British_Rail_Class_466)
• Ice/water is pulled from some sort of dimensional storage/through a portal/similar like dimension like travel.
  • While it’s technically possible for dust can be used to create portals there is little to no way to reasonably calculate any of this and it’s only second from the top due to the fact that if it were done it would assumedly take up less energy than the worst-case scenario.
• Ice is made from nothing but energy.
  • This is ridiculous not only in the capacity of the energy that would be required, but in the energy which would be released which would then need to be dissipated in some way. Even assuming that energy released is used to create the energy to create ice in the most efficient way possible, it would still require the dissipation of a ridiculous amount of energy before the molecules could be cooled down into ice.

The only way to continue from here is to take the “best” and “worst”-case scenarios and assume that it is somewhere in the middle. Hopefully towards the lower end because, as suggested to above, the worst-case scenario is ridiculous. 

4. “Best” case scenario

We don’t need to worry about where the water molecules where are coming from, nor do we need to worry about their temperature, they are already cold enough to freeze, we just need to make them into a form recognisable as ice.

We need to have 38696.72 ml of ice. The density of ice is 0.9340 g/cm³ which gives 36.14 kilogrammes of ice. While water vapor does exist at 0 degrees Celsius and below for the sake of making this the very best of best-case scenarios we are going to assume that instead of a gaseous state the water molecules appear close enough to be treated as a liquid. (High pressure gases turn back into liquids). So there is still some energy requirement we aren’t going to assume it appears as ice already so all we need to be concerned in this case is the Enthalpy of fusion for water. Which is  333.55 J/g. So 12,054,497 Joules of energy is subtracted from that amount of water to turn it into ice. Now we need to figure out how much energy the dust would have in it to freeze that much water as negative energy isn’t technically a thing. Thankfully heat pump’s exist, requiring energy to move heat into or out of a system and are relative nice to determine the efficiency of.

Cooling Efficiency (%) = %

As we have already declared the assumption of 0 degrees Celsius we have T_C = 273.15 K all that’s needed is T_h or the temperature of where the energy is being moved to. Assuming the train is at room temperature (T_h = 300) 

Cooling efficiency = 1017%

i.e. For every 1 joule of energy used to pump heat 10.17 joules of energy are moved. Now following some simple maths:

1,185,299.607 joules of energy are required to freeze that much water. Which for reference is approximately the calories gained by eating a sinkers bar. So while this may not sound impressive at first it is important to remember how big this much dust was. 3ml. Less than a teaspoon. This translates to 395,099,869,000 pascals or 395.1 MJ/L (which is more frequently used for the energy density of fuels. How does this relate to other things. Well assuming you could digest dust you could eat a days worth of calories on two tablespoons. Assuming lightning dust is comparable to ice dust you an AA battery sized piece of dust would last 303 times longer. If you could fill your car with dust instead of petrol the same sized tank would last 11.5 times longer. The amount of dust Weiss gave Blake in the scene which inspired this calculation is the same as giving someone 7 grenades. Makes a teaspoon’s worth of dust more powerful than a grenade. Stuff is powerful, but not excessively so. 

 (https://en.wikipedia.org/wiki/Energy_density)

(https://www.translatorscafe.com/unit-converter/en/energy/1-58/joule-kilogram%20of%20TNT/)

(https://www.quora.com/How-many-joules-does-an-M67-grenade-produce)

100.756607L X 0.93400.9340g/cm^3 = 94.1066709kg
94.1066709 kg X 333.55 J/g = 31,389,280.1J
31,389,280.1J/10.17 = 3,086,458.22J
3,086,458.22J/3ml = 1,028.81941 MJ/L
AA battery: 791 times longer
Car: 30 times further
Weiss gave Blake: 19 grenades

5. “Worst” case scenario

I am just going to go and say we need 36.14 kilogrammes of ice. E=mc² . Boom we need 3,248,101,220,000,000,000 Joules which translates to a 1,082,700,410,000,000,000,000,000 pascals or 1,082,700,410,000,000 MJ/L which makes it 740251127 years worth of calories on a teaspoon, AA batteries last 250,625,094,900,000 times longer, cars go 31,657,906,730,000 times further and Weiss gave Blake the equivalent of 19,407,870,300,000 grenades.

Truth be told this is far too simplistic and I’ve skipped over so many things in order to make this assumption.

• You can’t just make only matter from energy, you have to make anti-matter as well, this doubles the energy requirements.
  • This doesn’t even go into what happens to the anti-matter
• If we are being strictly scientific you can’t just make water molecules straight out from energy you need the atoms. Now hydrogen is easy, oxygen however requires multiple protons and neutrons and the mass of these protons and neutrons seperately is more than if they are in an oxygen atom. This increases the required mass to be generated by 0.75%. This may not sound like much but keep in mind how big the numbers are here.
• The process of making the oxygen atom from it’s constituent parts releases this “missing mass” (mass defect in science words) as energy. This energy will need to be taken away.
• We also need to add electrons to our atomic nucli, which will release energy which will need to be taken away
• Reacting oxygen and hydrogen together is literally rocket fuel, the energy released from this process will need to be taken away.
• Now converting from water vapor to ice will require energy to be taken away in a similar manner to that described in the “best” case scenario.

Now while I could do the full in depth analysis ultimately I find that there is little point. The numbers have lost all measure of scale. When I say a car would run eleven and a half times further on a tank of fuel you can picture that in your head. When is say the car can run thirty-one trillion, six hundred fifty-seven billion, nine hundred six million, seven hundred thirty thousand times further you loose all sense of scale. So rather than make this number any bigger with some technically speaking rather complex maths. I’m going to attempt to give context to this already rediculous number. The dust Weiss gave Blake if it were to say explode instead of be activated in the controlled way dust normally is would have a recommended safety distance of 2,171,065 meters. Still doesn’t sound real. No worries. There’s a website that lets you play with that: (https://www.mapdevelopers.com/draw-circle-tool.php?circles=%5B%5B2171065%2C2.5523516%2C-4.3608394%2C%22%23AAAAAA%22%2C%22%23000000%22%2C0.4%5D%5D)

Note that this neglects the fact calculations start getting odd at this sort of size so there’s no guarantee the “safe” area would be safe either. Especially with the damage to the earth itself taken into consideration.

(https://www.un.org/disarmament/un-saferguard/explosion-danger-area/)

94.1066709kg
8,457,885,780,000,000,000 J
2,819,295,260,000,000 MJ/L
AA batteries: 2,168,688,700,000,000 times longer
Cars: 82,435,534,000,000 times further
Weiss gave blake: 53,487,543,000,000 grenades
Blast radius: 3,043,904 meters
Website:

(https://www.mapdevelopers.com/draw-circle-tool.php?circles=%5B%5B3043904%2C0.4315417%2C5.4239039%2C%22%23AAAAAA%22%2C%22%23000000%22%2C0.4%5D%5D)

A realistic attempt.

Now the writer in me want to leave you with that revelation to deal with. The Physicist in me must continue. I want a reasonable value for energy density. And a range from 395.1 MJ/L to 1,082,700,410,000,000 MJ/L is simply far too large to assume that the answer is somewhere in the middle. Especially when logic states that its most certainly towards the lower end of the scale. Moreover I have overlooked a number of smaller things. Both the dust crystals for both the best and worst case scenarios would have comparable weights (and would be exceptionally heavy for their size). While the best case implies that ice dust is made of water there are no suggestions as to how this happened and as for what the worst case could be made of while I have a few ideas none are pratical, being prone to detonating in the way described simply by existing.

So I have decided that rather than leaving things as they are I want some sort of middle of the scale value. So we are going to take the “most physically reasonable” method of making that much ice and run the numbers one last time. As for what the “most physically reasonable” case is. Personally I’d say it’s the freezing of water vapor method. It’s not completely without its issues but second most practical involves portals and I’m not willing to go into the maths behind that.

I’m going to try doing this in the most energy efficient way possible. This results in the slightly odd method so we are going to start with the specific gas constant for water vapor:

We know the mass of ice required is 36.14kg and we know the kelvin values for room temperature and 0 degrees Celsius are 300K and 273.15K respectively. So we can work out the energy required to take water vapor at room temperature down to water vapor at 0 degrees Celsius. It is worth particular note the triple point of water (where water is a solid liquid and gas simultaneously) is 273.16K so we will only be going this far instead.

To work out the cooling efficiency I will need the average value of (T_c / (300 – T_c)) for all values of T_c between 275.16 and 300. Now I don’t feel like doing integrals in my working but thankfully computers are a thing so I’m going to simply find the average value in that range:

0.0372578 Integrate[x/(300 – x), {x, 273.16, 300}]

Returns a result of so

From Gas to liquid using the Heat of vaporization

Just going to assume the cooling efficiency from the best case scenario as a 0.01K change isn’t going to result in a 1% change to cooling efficiency so:

The specific heat of water

Just going to assume the cooling efficiency with the same logic as the previous section

From Liquid to Solid was done in the best case scenario already so:

Following the same pattern as the previous two sections:

• 3,084,120,926,000 pascals
• 3084.12093 MJ/L
• 5 years worth of calories on a teaspoon
• AA batteries last 713.8 times longer
• Car goes 90 times further on a tank of fuel.
• Weiss gave Blake the equivalent of 55 grenades.

This may pale in comparison to the worst of worst case scenarios but we always knew that the energy requirements would hopefully be towards the lower end of this scale. So it may not be as ridiculous in comparison to the worst case scenario but this is still ridiculous on the scale of things here on earth. So for the sake of comparason:

• Tritium reactors (theoritical): 158 MJ/L
• Remnant dust (Best case): 395 MJ/L
• Remnant dust (Realistic case): 3,084 MJ/L
• Deuterium reactors (theoritical): 15,822 MJ/L
• Plutonium reactors: 43,277,365 MJ/L
• Uranium reactors: 1,529,842,000 MJ/L

Why is dust ridiculous if we have fuel sources with a higher energy density? Multiple reasons:

1. Dust is pleantiful on Remnant. We see massive islands floating in the sky held up by dust, enviroments (presumably based off of realistic, on planet, ecosystems) where dust litters the ground. You can walk into a shop and flat out buy dust. Not only are their multiple of these stores in a single city but they have no security greater than a single cashier. The same cannot be said for any of the above real world materials.
2. Dust is clean. From what we see of it it makes whatever the dust is named after (ice from ice dust, fire from fire dust, lightning from lightning dust) and leaves nothing else behind. Nuclear reactors have major issues with their waste products. Plutonium and Uranium reactors have waste thats dangerous for thousands to millions of years and while Tritium and Deuterium waste may only be dangerous for 50 years in comparason during that time the waste is actually more dangerous than those from Plutonium and Uranium reactors.
3. The people of Remnant just walk around with dust on their person. In their weapons, clothes, pockets, bags, tools, so on and so forth. Probably because just how convenient, safe, powerful and common it is. The reason we don’t walk around with nuclear fuel on our person is mainly safety but also to do with the fact it’s difficult to use as a fuel source properly. Sure you’d only need around a quarter of a litre of weapon grade plutonium to get an explosion but that isn’t exactly controllable. On the other end of the spectrum people in Remnant probably don’t use batteries. To demonstrate why if your phone normally lasts 10 hours on Remnant it would last somewhere between 1.5 and 4 years (depending on phone). That and the charging process for chemical batteries (from say lightning dust) is only going to waste energy anyway.
4. Dust comes in types. If you wanted say ice you’d simply use ice dust on remnant. On earth you need to get power from somewhere, (let’s say a nuclear power plant), which induces energy loss and requires specialist equipment, get energy from the generator to where you are, which induces energy loss and requires a physical connection, convert the power into a cooling mechnisim, which induces energy loss and requires more equipment, then wait as ice is made, energy loss over time and loss of time. That and some of the types of dust on Remnant can do things which we on earth simply cannot do. Indeed the stuff you could do with gravity dust alone warrents a similar analysis in and of it’s own right and hard light dust is unique in what it is capable of.

So the writer in me want’s to leave you with this shocking fact. The scientist in me want’s it to be accurate. They’ve came together and come up with this. The average American will use 2025MJ of electricity over the course of their entire life. This means in a “realistic” case you could walk to the dust store, which has no real world equivalent but I have come to the conclusion it is some form of jewlery store which also sells comics and pick & mix. You could then leave the dust store the same day with a container, about the size of 2 pints of milk, and in that container would be all the electricity you will ever need for the rest of your life.